2023. 12. 21. 12:46ㆍCS/데이터베이스

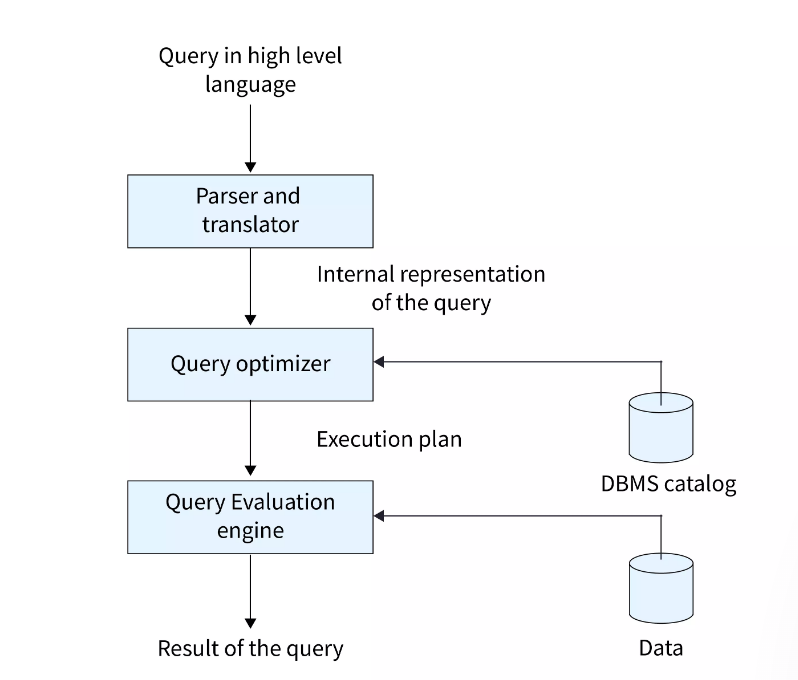
Parser가 적절한 Procedure Language (Linear Algebra )로 쿼리를 변환하고,
DBMS catalog 을 이용하여 Query Optimizer 를 실행합니다.
왜 최적화 (Optimization)를 진행하는 걸까요 ?
What is Query Optimization ?
Query Optimization 이란, 최적화된 쿼리 실행 계획입니다. DBMS는 실행 계획들 중에 최소 Cost 를 가지는 Query plan 을 실행합니다.
왜 이런 일을 진행하는 걸까요? 생각해보면 상당히 심플한 아이디어에서 접근합니다. 우리는 절차를 수행하는 방법을 순서에 따라 명확하게 나타낸 것을 ‘알고리즘’ 이라고 합니다. 알고리즘은 같은 문제에 대해서 어떻게 접근 하는지에 따라, 최적 시간 내에 풀이가 가능하기도 하지만, 어떤 경우는 굉장히 복잡한 시간 내에 해결하는 풀이를 작성하기도 합니다.
이러한 아이디어를 쿼리 수행에 빗대어서 생각해 본다면, DBMS는 최적 시간 내에 사용자가 입력한 쿼리를 수행하기 위하여, 나름의 최적화를 진행한다고 생각하면 되겠습니다.
HOW?
그렇다면 어떤 방식으로 최적화가 가능한지에 대해 궁금하실 겁니다.
아래는 대략적인 예시입니다.

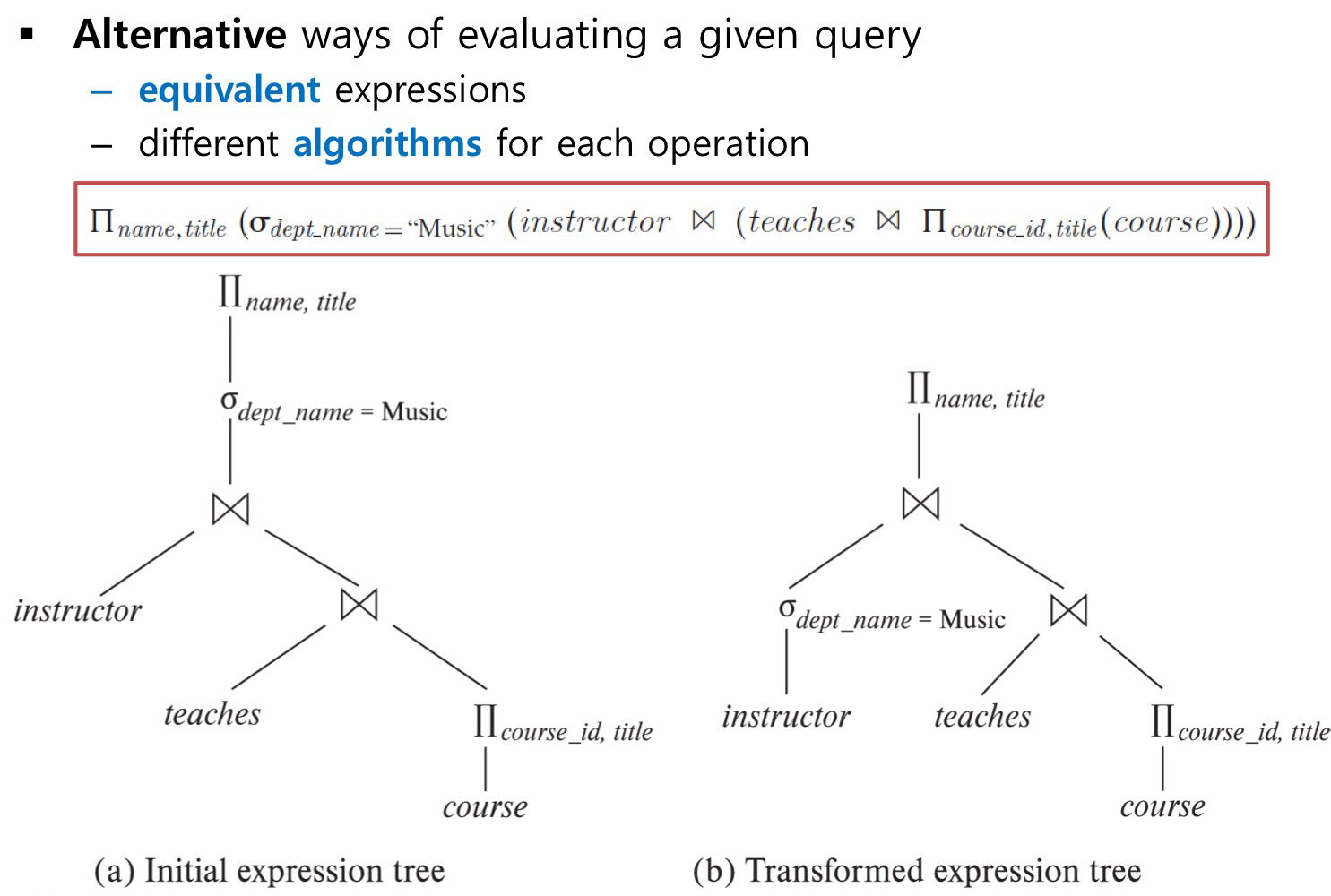
모양이 꽤나 복잡합니다.
천천히 같이 보겠습니다.
위 쿼리는
- Course table 에서 course_id, title 을 Projection
- teaches table 과 natural join
- 그 결과를 instructor table 과 natural join
- 그 결과중 dept_name 이 “Music” 인 tuple 선택
- 선택된 tuple 중 name, title 만 추출
의 형식으로 진행됩니다.
아래에 트리는 expression tree 로, 쿼리의 논리적인 진행 순서를 도식화 하여 표현한 형태입니다.
(a) 번을 보시면 위에서 말한 흐름대로 진행하고 있습니다.
Course_id, title 을 뽑아서 teaches 와 natural join 하고.. 등 동일합니다.
이제 (b)번을 보시면 형태가 조금 달라짐을 알 수 있습니다. 기존에 윗부분에 있던 dept_name = “Music” 을 왼쪽 아래 Instructor 칸으로 내린 것을 확인 할 수 있습니다. 형태가 달라진다고 해서 실행 시간에 영향을 미칠까요 ?
정답은 '네' 입니다. 이전 포스팅에서 살펴보았듯이, join 연산은 nested loop join , 쉽게 말하면 이중 반복문으로 진행됩니다.
따라서 미리 dept_name = Music인 튜플을 골라놓으면 반복문에 참여할 튜플이 적어져 더 효율적인 연산이 가능합니다.
이러한 최적화 작업이 우리가 쿼리를 보낼 때 마다 일어나고 있습니다.
이러한 비용을 기반으로 일어나는 최적화를 Cost based Optimization 이라고 부릅니다.
인간은 이렇게 한눈에 볼 수 있는데, 기계는 그렇지 못하죠. 어떤 방식으로 결과를 도출할까요 ?
Cost based Optimization ?
다음은 Cost based Optimize 를 진행하는 단계입니다.
- Equivalence rules 를 사용해서 논리적으로 동등한 표현식들을 만듭니다.
- 결과 표현식에 주석을 단다. 다른 대안의 쿼리 플랜을 얻기위해
- 가장 저렴한 비용을 가지는 플랜을 실행한다.
두 쿼리가 Equivalent 하다. 라는 것은, 두개의 관계대수 식의 결과가 같다면(같은 튜플들의 집합을 도출한다면) 두 관계대수 식은 Equivalent 하다고 합니다.
Equivalence Rule 은 동등성 규칙으로써, 쿼리를 어떻게 수정하여야 Equivalent 한지에 대해 정리한 규칙입니다.
Equivalence Rules

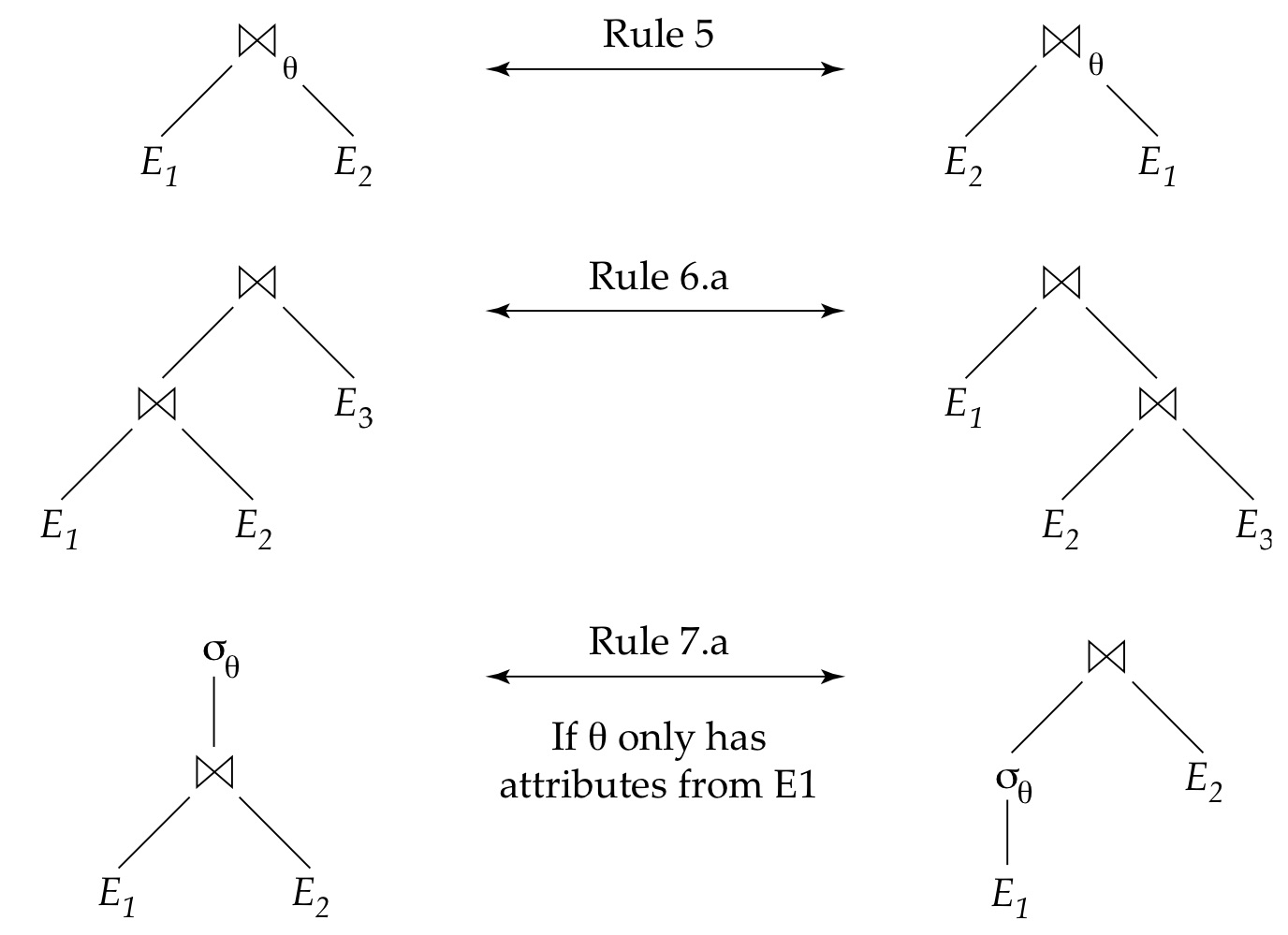


처음은 간단한 규칙입니다. 각각 살펴보자면
- 두개의 selection 은 개별적인 selection 으로 나눠질 수있다.
- Selection 연산은 교환이 가능하다. (즉, 어떤 것을 먼저 수행해도 실행 결과는 같다.)
- Projection 연산은 오직 가장 마지막에 수행한 연산만 살아남아 표현된다. (Projection 은 중복을 제거합니다.)
- Selection 연산은 Cartesian product 와 theta join 으로 표현될 수 있다.
(4.b 번은 조금 모호하지만, 𝝈dept_name = “Comp_sci” (Instructor ⨝(t_id = I_id) Teaches) = Instructor ⨝(dept_name=Comp_sci and t_id = i_id) Teaches와 같이 예시를 들어 생각해본다면 비교적 이해하기 쉽습니다.)




- 두 natural join 의 순서는 바뀌어도 된다.(교환 가능하다.)
- ( E1 ⨝ E2 ) ⨝ E3 이나 (E2 ⨝ E3) ⨝ E1 의 결과는 같다.
- a. 𝝈θ (E1 ⨝ E2) 나 𝝈θ (E1) ⨝ E2 의 결과는 같다. (단, θ 조건이 E1 과 관련되어 있을 때에만!) 이 되겠습니다.
주의할 점은 마지막 예외인데요, 생각해보면 간단합니다. 예를 들면 ID, dept_name, salary 가 있는 table 에서 쌩뚱맞게 다른 attribute인 name 을 select 하면 안된다는 뜻입니다.
b. θ1 조건이 E1 테이블과 연관이 있고, θ2 조건이 E2 테이블과 연관이 있을 경우에 다음과 같이 치환이 가능합니다.


- a. θ조건이 L1과 L2 attribute 의 합집합인 경우에만 적용될 수있는 규칙입니다. 각각 L1, L2 조건에 대해 Projection 연산을 먼저 수행합니다. 그 후 Natural join 을 실행함으로써 반복되는 튜플들의 개수를 줄일 수 있습니다.
b. E1과 E2가 θ조건을 가지는 natural join 을 실행하는 경우에 생각해 볼 수 있는 방법입니다. L1 과 L2 는 기본적으로 E1, E2에 속하는 attribute 입니다. 하지만 특이하게 L1 L2 엔 속하지 않지만, Join 에는 참여하는 L3 과 L4가 등장합니다. 슬슬 이쯤부터 머리가 아파지는데요, 예시를 보겠습니다.
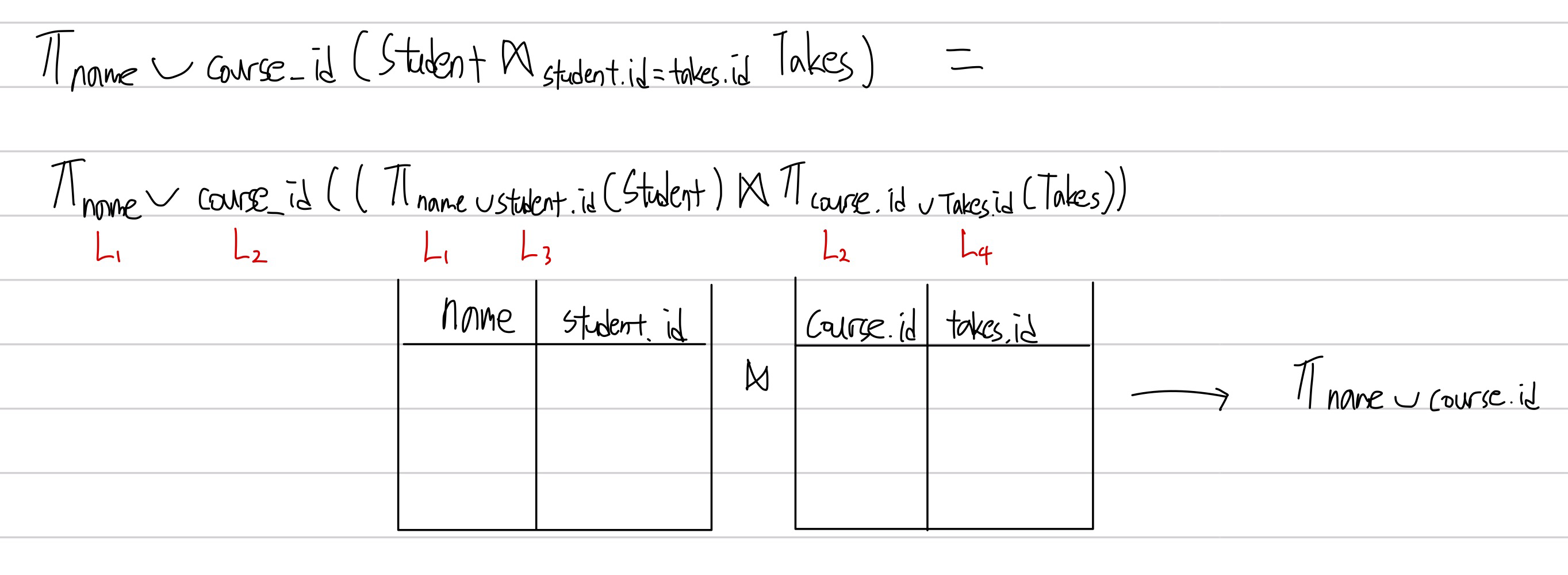

예시입니다.

- 집합 연산 중 Union(합집합) 과 Intersection (교집합) 은 교환이 가능하다.
- 또한 결합법칙도 적용이 가능하다.
- Selection 연산은 합집합, 교집합과 - 연산으로 분해가 가능하다.
(교집합의 경우는 - 로 표현이 가능하지만, 합집합은 그렇지 않다. ) - Projection 연산은 합집합으로 분해가 가능하다.
이렇게 Equivalence rule 들이 존재합니다. 이러한 equivalence rule 들은 최소한의 연산들로 쿼리를 실행하려고 합니다. 내가 만들어낸 연산이, 다른 연산으로 부터 도출된다면 경우의 수가 매우 많아지기 때문입니다.
따라서 Query Optimizer 는 Equivalence rule들 중의 minimal sets 들을 사용해 쿼리 실행 계획을 생성합니다.
지금까지 Query Optimizer 가 Query plan 을 단순하게 생성하는 방식을 알아보았습니다. 하지만 정말 이런 방식들이 효율적일까요 ?
Query Optimizer 는 Equivalence rule 을 이용해 발생하는 쿼리들에 대해 무식하게 모든 표현식을 생성해냅니다. Minimal 한 Plan도 여러개가 존재할 수 있기 때문입니다. 그렇다면 결국에 이러한 방식은 Brute Force 기법에 지나지 않습니다.
그래서 DBMS Community는 추가적인 방법을 고안해 냅니다. 바로 통계 추정치인 휴리스틱을 이용해 계산하는 방식입니다.
현재까지 정리하자면, Query Optimize plan을 생성하는 방법에는
- Equivalence rule 을 따라 무조건적으로 plan 생성
- 통계치를 사용하여 나온 근사값으로 계산
이렇게 두가지 방법이 있고, 이제 2번 방식에 대하여 알아보겠습니다.
Statistics for Cost Estimation

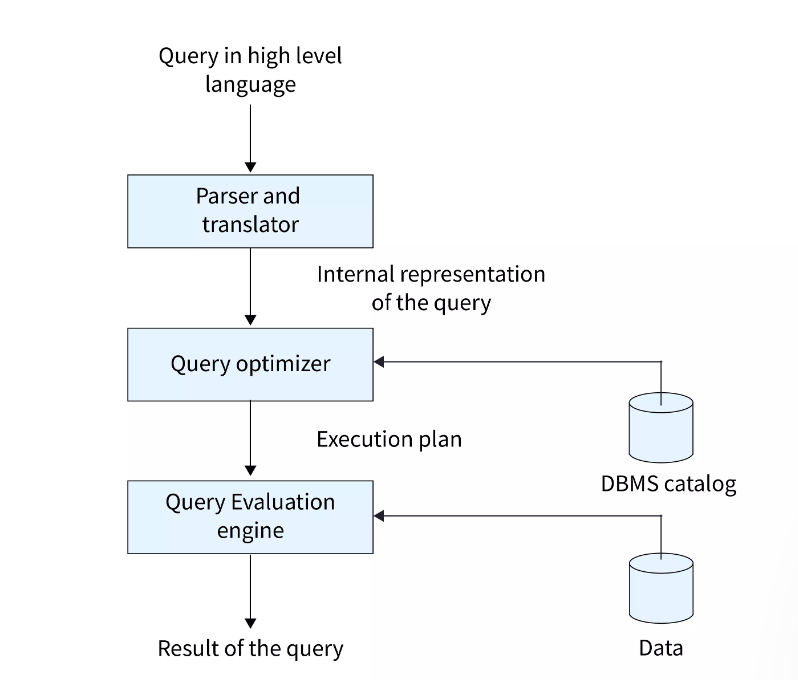
위 그림에서 보이듯이, DBMS에는 catalog 가 존재합니다. 이곳에 테이블의 대략적인 통계 정보를 저장하고, 필요시에 사용하는 방식을 택합니다.
그렇다면 이 추정치가 정확한지에 대해 의문을 제기할 수 있겠지만, 현재까지 나타난 결론은 상당히 정확하며, 특히 데이터가 잘 변하지 않는 OLAP (Data Warehouse) 같은 경우에 특히 잘 적용될 수 있다고 합니다.
그럼 통계 정보를 이용해서 쿼리를 수행하는 과정을 순서대로 알아보겠습니다.


다음은 DBMS 가 대략적으로 통계정보를 저장하는 방식입니다.
Nr : relation r이 가지고 있는 튜플의 개수입니다.
Br : relation r이 가지고 있는 block 들의 개수입니다.
Lr : relation r의 튜플 사이즈입니다.
Fr : Blocking factor 로서, 한 블록에 들어가는 튜플의 개수입니다. 즉 Br = Nr/Fr 로 표현이 가능합니다.
V(A,r) : relation r에 나타나는 중복이 없는 Attribute A의 개수입니다. Projection 을 생각하면 이해하기가 쉽습니다.
예를 들어보자면, instructor table 에서 학과명이 구분되는 개수는 V(dept_name, instructor) 로 표현이 가능합니다. V(dept_name, instructor)=10이면, 전체 tuple 의 개수가 100이라고 가정할 때,
100 x 1/10 , 즉 10%의 확률로 특정 학과의 학생임을 추정할 수 있습니다. 또한 중복이 제거된다는 점을 잘 기억해주세요 .


위에서 얘기한 내용과 비슷한 맥락입니다. 정확한 통계정보를 위해서는, relation이 수정될 때 마다 update 가 필요합니다. 하지만 이러한 방법은 상당한 양의 오버헤드를 불러 일으키고, DBMS는 이러한 방식을 사용하지 않습니다.
대부분의 시스템에선, 매 변경시마다 통계정보를 수정하지 않습니다. 대략적인 근사치를 통해 계산을 진행하다 System Load 가 적은 시기에 update 를 진행한다고 합니다.
물론 이러한 방법은 굉장히 정확한 방법은 아니지만, 너무 많은 업데이트가 발생하는 것이 아니면 충분히 정확하다고 할 수 있습니다.

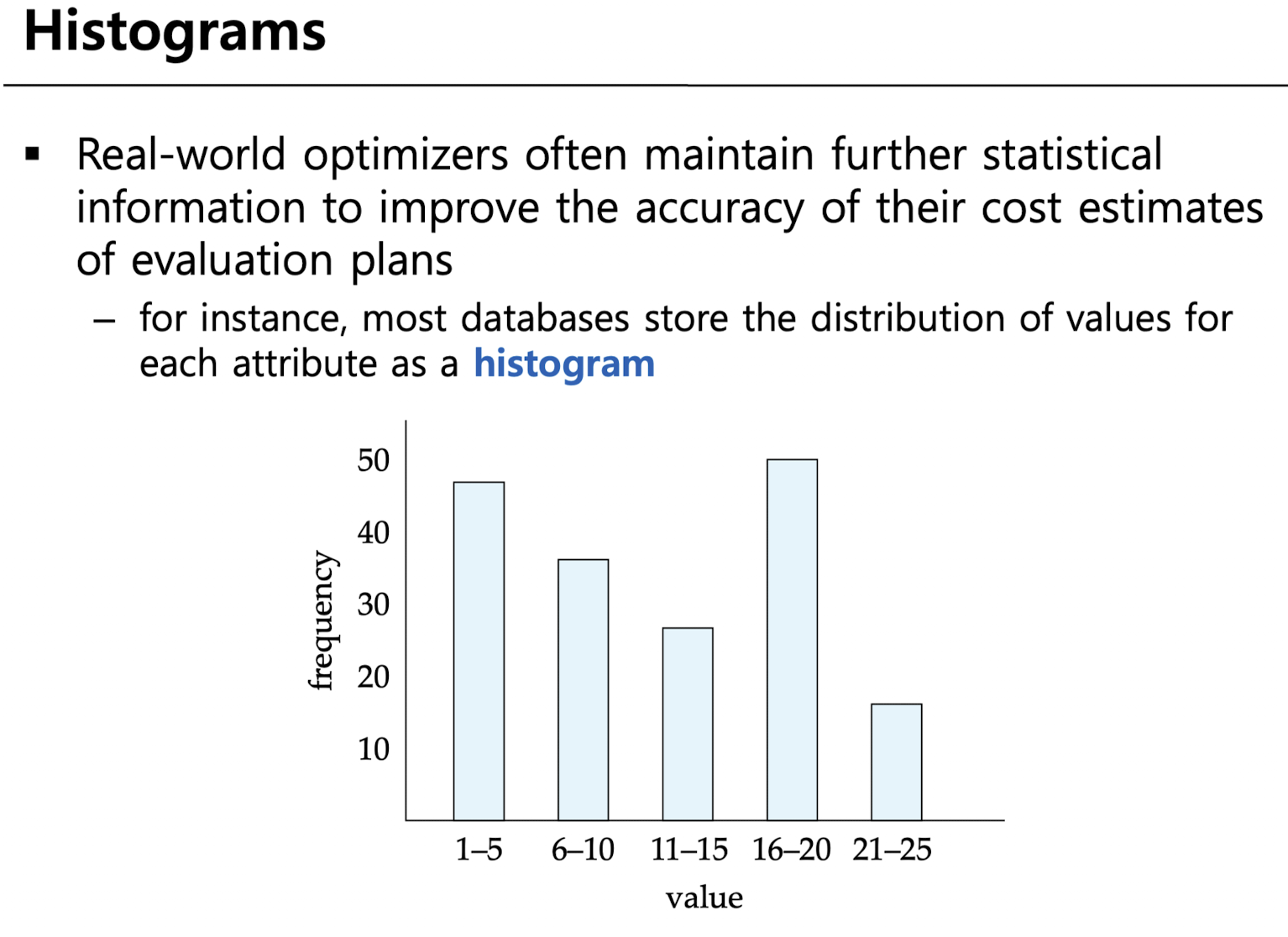
또한 현실의 Optimizer 는 조금 더 정확한 정보 저장을 위하여, 도식화된 Histogram을 사용합니다. 통계 분포가 있다면 조금 더 정확한 정보 저장이 가능할 것입니다.
Selection Size Estimation
통계 추정치를 이용해 실행 계획을 계산한다는 것은 알았습니다. 그렇다면 어떻게 계산이 진행되는 걸까요 ?
이 연산 또한 각 연산의 종류에 따라 차이가 있습니다. 먼저 Selection 입니다.


- A=v, 어떤 조건에 대하여 동등성을 구하는 연산입니다.
이 방식은 가장 단순한 selection 연산으로, Nr/ V(A,r) 로 계산합니다. 예시를 들어보겠습니다.
V(dept_name, instructor) = 10 , Nr = 100 인 경우, instructor table 의 중복이 없는 dept_name의 개수는 10개 입니다. 즉, 독립된 학과 10개가 존재한다고 생각할 수 있겠습니다.
Nr * 1/10 = 10 입니다. 전체 튜플의 개수를 곱함으로서 대략적으로 각 학과당 몇명이 존재하는지를 추정할 수 있습니다. 하지만 위에서 말한 조금 더 정확한 방법인 Histogram 이 존재하는 경우, 조금 더 정확한 연산이 가능합니다.
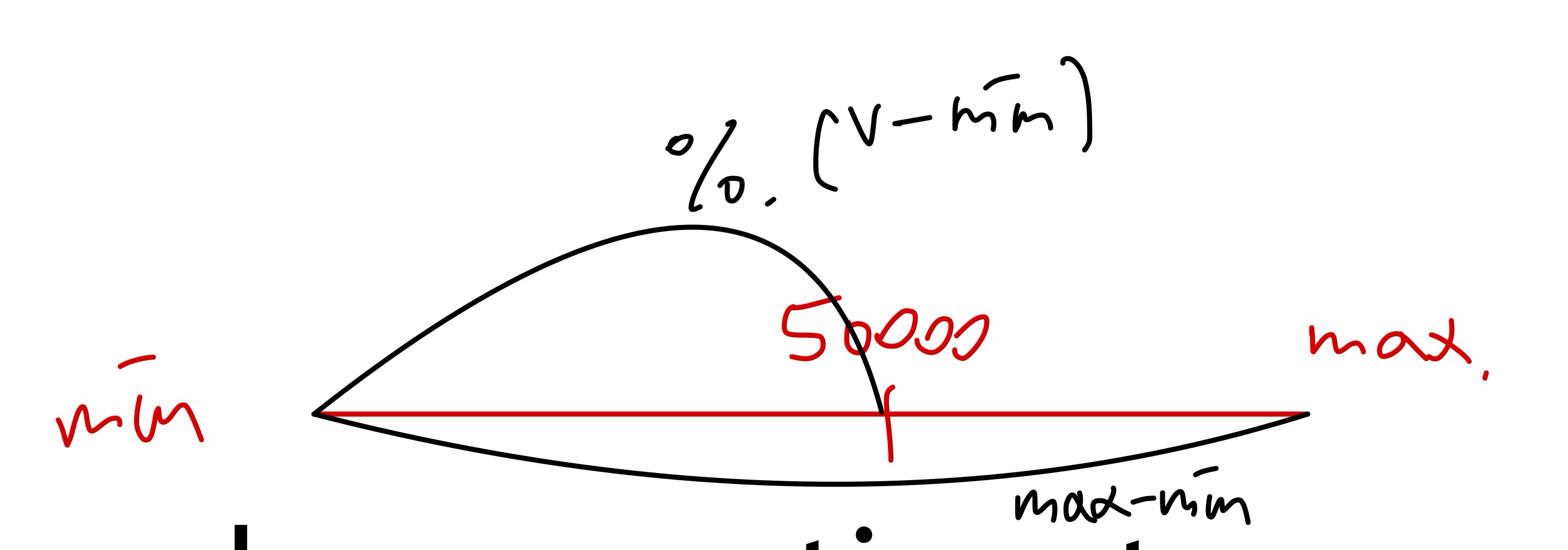
- 다음은 A<=V (A>=V) 대소 비교입니다. c를 조건을 만족하는 튜플의 개수로 가정하겠습니다.
만약 조건이 min(A,r) 보다 작다면, 즉 기존에 존재하는 값 보다 적은 값을 요청하는 경우는 c = 0 입니다. 그렇지 않을 경우, c는 Nr * (V- min(A,r)) / (max(A,r) - min(A,r)) 로 계산이 가능합니다. 어떻게 이런 연산이 나올 수 있는지 보겠습니다.
단일 연산 Selection의 경우에 대해서 알아보았습니다.
Size Estimation of Complex Selections
다음은 Complex Selection의 경

우입니다.

선택 condition θi 의 경우, relation r의 tuple 이 조건을 만족하는지에 대한 확률로 표현합니다. Si 가 조건을 만족하는 튜플들의 개수라고 가정하고 θi 가 주어진 경우에는 Si/Nr 로 계산합니다.
또한, 조건에 and 절이 포함 된 경우는 이러한 각 확률들의 전체 곱 * 튜플들의 개수로 계산됩니다.
𝝈salary <= 5000 ∧ dept_name = ‘Comp_sci’ (instructor)인 경우, 대충 salary <= 5000를 만족하는 확률이 1/3, 대충 dept_name = ‘Comp_sci’를 만족하는 확률이 1/10 이라고 할 경우, 동시에 만족할 확률은 1/30이 되고.
전체 튜플의 개수가 100개라고 가정할 경우 해당 selection 조건은 100 * 1/30 으로 연산이 가능합니다. 확률 산수같은 느낌입니다.


Or 연산의 경우 조금 더 복잡한 형태입니다. 1-조건을 충족할 확률 => 조건을 충족하지 않을 확률입니다.
조건을 충족하지 않을 확률들을 곱한 후, 1에서 뺀 후, 튜플들의 개수를 곱하여 계산합니다. 이 또한 단순한 확률 계산 문제이므로 넘어가겠습니다.
부정 연산의 경우는 조금 단순합니다. 조건을 만족하는 튜플의 사이즈를 구한 후 , 전체 튜플에서 제외하기만 하면 됩니다.
Join Operation : Running Example
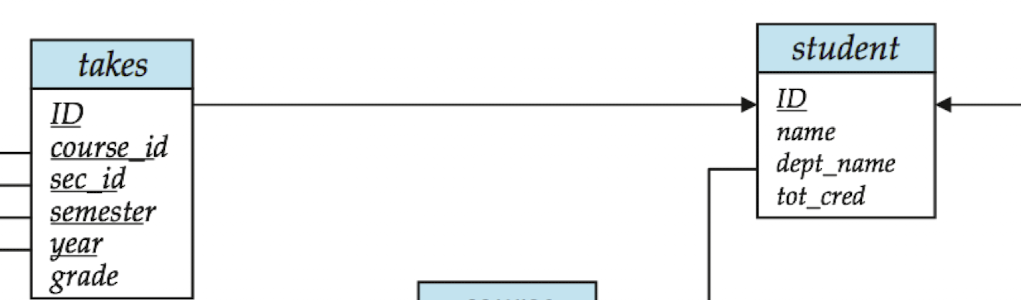



실제 예시를 통해, Joins 연산의 경우를 살펴 보겠습니다.
V(ID,Takes) = 2500입니다. 이 뜻은, 평균적으로 각 학생은 4개의 수업을 듣는다는 뜻이 됩니다. (10000 * 1/2500)
또한 V(ID, student) = 5000으로서, 학생은 5000명이 존재한다는 사실을 알 수있습니다.
왜 5000명일까요 ? 바로 ID는, student 테이블의 primary key 입니다.
Takes의 ID는 PK가 아니므로 중복이 가능합니다. 하지만 그 중 독립된 값만 추출했을 경우가 2500개인 경우이기 떄문에, (10000 * 1/2500)의 연산이 가능한 것입니다.


r과 s, 두 테이블을 Cartesian product 시 모든 경우의 수를 곱하고, 이는 곧 각 튜플이 Ir + Is byte를 가짐을 의미합니다.
ex) R = (name, ID) , S= (age, gender) , r x s = (name, ID, age, gender)가 되겠죠?
그 아래 내용은 어찌보면 당연한데요, R 과 S에 공통 분모가 없다면, r natural join s 는 그냥 둘을 단순히 cartesian product 한 것과 다름없습니다.
하지만 만약 R 과 S의 공통 분모가 R의 Key인 경우에 s의 튜플들은 r의 튜플들과 ‘많아봐야’ 1개씩만 join이 일어납니다. 그 말인 즉슨 , s 튜플의 개수 이하만큼만 결과로 도출될 수 있음을 의미합니다.


다음 경우입니다. R 과 S의 교집합이 Foreign key 인 경우입니다. 교재에서는 S가 R을 참조하는 형태인데요. 이 경우는 Null이 아니란 가정 하에, 결과값이 무조건 S의 튜플 개수와 같아집니다. 왜 그럴까요?
Foreign key에는 Integrity Constraint가 존재합니다. 그 말인 즉슨, 참조하는 쪽에서 값이 존재한다면, 참조 당하는 쪽에 무조건 해당 값이 존재해야 한다는 뜻이 됩니다.
(주소가 100번지로 찍혀있어서 찾아가봤더니 실제 값이 존재하지 않는 그런 경우는 허용하지 않는다는 뜻입니다. )
때문에 foreign key 는 , null 값도 허용합니다. 하지만 null인 경우에는 값을 체크할 수 없으므로 해당 계산을 수행할 때는 foreign key가 null 이 아니라는 가정이 필요한 것입니다.
이러한 가정 아래, foreign key 에 대한 Join은, 참조하는 relation의 tuple 개수와 일치하게 됩니다.


항상 key 에 대해서만 Join 이 일어나는 것은 아닐 겁니다. 공통 분모가 R과 S의 키가 아닌 경우에 대해서 살펴보겠습니다.
이 경우, 양쪽 모든 값에 대해 계산이 필요하고, 그 중 최소값을 취하는 전략을 택합니다.
s의 튜플 개수 / s 테이블의 Distinct한 A 개수 를 평균 추정치로 계산할 수 있습니다. 그 값에 상대 tuple 개수를 곱함으로서, join 시의 추정치를 구할 수 있습니다.
이 경우는 상대방에 대한 계산까지 진행 한 후, 최소값을 택합니다. 최소값이 더 정확한 결과가 되겠습니다.
Size Estimation for Other Operations




다른 연산들의 경우입니다. Projection과 Aggregation 의 경우, V(A,r) 의 정의와 똑같습니다.
그 외 서로 다른 relation의 경우 합집합은 각 relation size 의 합으로 표현이 가능합니다.
또한 r과 s의 교집합은 위의 사례와 비슷하게, r 과 s의 최소값으로 표현이 가능합니다.
마지막으로 r - s 의 경우는 r로 표현이 가능합니다. 언뜻 보면 느낄 수 있듯이, 상당히 연산을 대충 진행하는 느낌입니다.
하지만 이러한 방법은 정확하지는 않을 수 있지만, 상한은 보장한다고 합니다.
Choosing Evaluation Plans
Evaluation plan은 쿼리 진행에 어떤 알고리즘이 사용되어야 하고, 어떻게 coordination 되어있는지 적혀있는 것입니다. Query Optimizer 가 최적 plan을 고르면, 엔진은 해당 plan을 이용해 실행하는 역할을 맡습니다.
Cost Based Optimizer 가 가능한 모든 쿼리를 탐색하며, 최소값을 찾습니다. 하지만 위에서 언급했듯이, 모든 경우의 탐색은 비용이 많이 들기 때문에, 대부분의 시스템에서는 휴리스틱을 이용하여 처리합니다.
기본적인 방법으로는 Dynamic programming 을 이용해 중복 경우의 수를 제거하여 계산합니다.
Dynamic programming


위와 같이 S1을 (S - S1) 과 Join 하는 연산을 재귀적으로 수행하며 비용을 계산합니다. 또한 memoization 을 사용하여, 이미 계산한 값은 다시 사용하는 모습을 볼 수 있습니다.
Heuristic Optimization


Heuristic 방식은 비교적 간단합니다. 비용 계산에 효과적이라고 알려진 규칙들을 적용함으로서, 결과를 계산합니다.
규칙들은 다음과 같습니다.
- selection은 빠를 수록 좋다.
- projection은 빠를 수록 좋다.
- selection 조건 여러개 중, 결과가 가장 작은 것을 먼저 실행 후, join혹은 selection 진행하면 효율적이다.
몇몇 시스템들은 오로지 heuristic 방식만을 이용해 비용을 계산하기도 합니다.

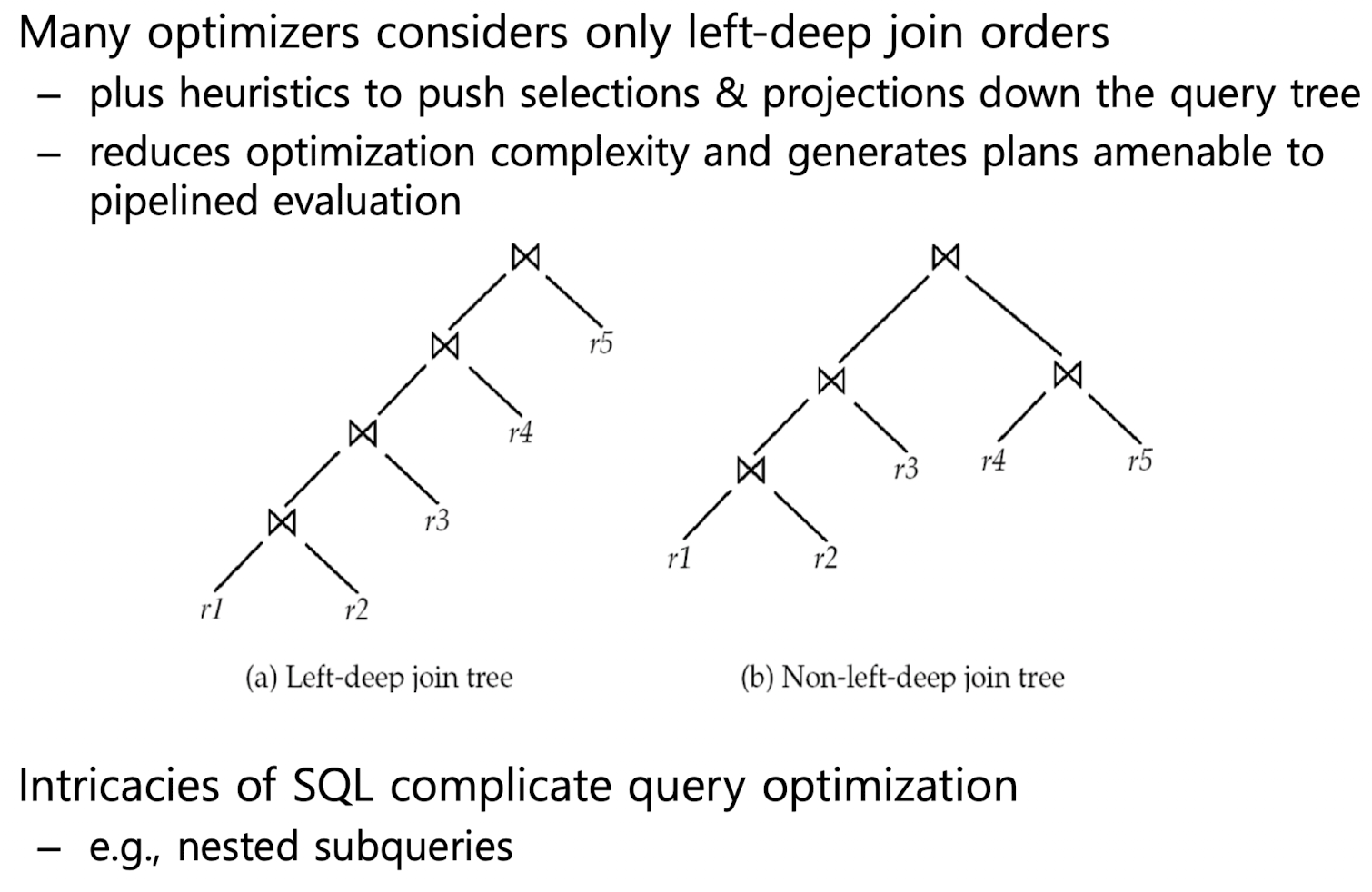
또한 많은 optimizer들은 오직 left deep join order 를 적용합니다. 이 방식은 Piped Evaluation에 더 적합한 방식이고, 연산 시에 복잡도도 감소하는 장점이 있습니다.


무심코 날린 쿼리들을 되돌아보는 시간입니다. Nested subquery 는 복잡한 작업입니다.
DBMS는 Nested subquery에 대해 1차원 적으로 계산하기 위해 평면화를 실행합니다. 그것을 decorrelation 이라고 부릅니다.
이 작업은 하위 쿼리와 상위 쿼리간의 종속성을 제거하는 작업이고, 변화한 모습을 보면 subquery에 대해 테이블을 새로 만들어 연산을 수행하는 것을 볼 수 있습니다.
Cost Based Optimization with Equivalence Rules


Physical Equivalence rules들은 query plan 들이 구체적으로 어떤 알고리즘을 이용하여 진행되는지에 대해 명시하고 있습니다.
Equivalence rule 은 논리적 동등성을 나타내며, Physical Equivalence rule은 물리적인 측면에서 쿼리의 실행계획과 최적화 규칙을 나타냅니다.
특히 dynamic programming 을 사용하는 형태는 가지치기를 사용하여, 모든 계획을 생성하는 것을 막고 있습니다.
Mysql 의 경우 EXPLAIN 명령어를 통해, 쿼리 실행 계획을 볼 수 있습니다.
EXPLAIN SELECT *
FROM employees e
INNER JOIN salaries s ON s.emp_no = e.emp_no
WHERE first_name='ABC';
Oracle 의 경우는 explain plan for 로 가능합니다.


알면 알수록 흥미로운 데이터베이스 입니다.
이상으로 DBMS 의 쿼리 비용 최적화 방법에 대하여 알아보았습니다.
다음 포스팅에서는 Database의 꽃인 트랜잭션에 대하여 알아보겠습니다.
감사합니다!
'CS > 데이터베이스' 카테고리의 다른 글
| Transaction (1) | 2024.01.16 |
|---|---|
| Materialization 과 Pipelining (0) | 2023.10.30 |
| Query Processing (1) | 2023.10.28 |